You often hear Type I and Type II errors in statistics classes. There is good reason for that — minimizing either of these two errors is pretty much the core of statistical theory.
Preliminaries
Type I and Type II errors are related to the concept of hypothesis testing. In hypothesis testing, we have two hypotheses:
01. Null hypothesis – the hypothesis of “no effect,” the status quo.
example: Income and gender are independent of one another.
This is a conjecture of no effect since it states that income and gender has nothing to do with each other.
02. Alternative hypothesis – the statement which we (usually) hope to prove.
example: Income and gender are associated.
Typically, the alternative hypothesis is the hypothesis which we intend to prove.
However, statistical tests of hypotheses are a form of a proof by contradiction.
To prove by contradiction is to assume the null hypothesis. Under this assumption, we attempt to show through evidence that the null hypothesis is implausible.
If we have shown this successfully, we are compelled to conclude in favor of the alternative hypothesis. We say that we reject the null hypothesis and that we have sufficient evidence in favor of the alternative.
On the other hand, if under the assumption of the truth of the null hypothesis, our findings are consistent, we cannot reject the hypothesis. This means that we do not have sufficient evidence supporting the alternative and that we fail to reject the null.
In other words, while we are interested in the alternative hypothesis, it is the null hypothesis which we put to the test.
What are Type I and Type II Errors?
Now, given this, we have four scenarios:
- We reject the null hypothesis when we should reject it.
- We do not reject the null hypothesis when we should not reject it
- We reject the null hypothesis when we should NOT reject it
- We do not reject the null hypothesis when we SHOULD reject it.
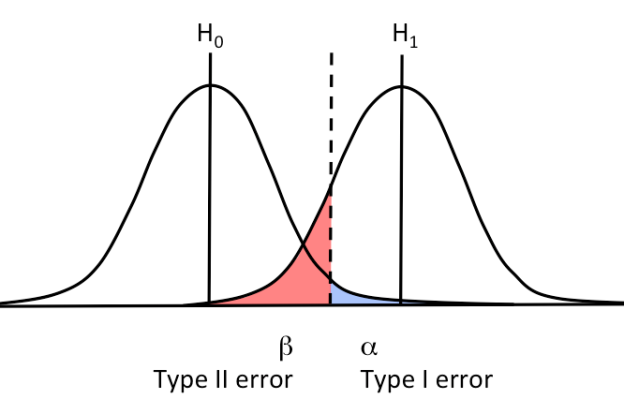
The first two are correct decisions. The last two are Type I and Type II errors, respectively. The diagram below simplifies the four scenarios we just laid down:
Why do I need to know about these errors?
A Type I error is a false positive. Meanwhile, a Type II error is a false negative. Ideally we want to minimize both errors.
There’s a catch though. Type I and Type II errors are inversely related. This means that minimizing one inflates the other.
To be able to know these type of errors will allow you to assess what kind of risk you are willing to take and what kind of risk you cannot afford.
An illustration
To put this into perspective, let’s look in the field of medicine, screening tests and diagnostic tests can illustrate the need for minimizing Type I and Type II errors well.
Screening tests are meant to detect true positives. This means that these tests should minimize false negatives — type II errors. By minimizing Type II errors, the screening tests can accurately detect most individuals who potentially have a particular disease.
People who tested positive in a screening test will have to undergo a diagnostic test. Diagnostic tests are meant to detect true negatives.
This test will verify whether a patient truly has the disease. In this case, we intend to minimize false positives — type I errors. A falsely diagnosed patient will end up undergoing treatment. This may cost them not only their money but potentially, even their lives.
Inevitable risk
The implications of Type I and Type II errors are widely encompassing. Statistics is applied not only in medicine but also in engineering, computer science, and the social sciences — just to name a few.
Statistics relies on probabilities. There is always a margin of error — a possibility that the wrong decision has been made.
We can never be absolutely certain in statistics. However, Knowing what type of error we can commit and just how probable this error can occur provides us confidence in our results.